List of Problems:
Chapter 4 Problem 12 - Classical Mechanics - T.Kibble, F.Berkshire
Chapter 4 Problem 29 - Classical Mechanics - T.Kibble, F.Berkshire
Chapter 5 Problem 11 - Classical Mechanics - T.Kibble, F.Berkshire
Ch.4 P12 - Distance of Closest Approach Problem
A star of mass \(M\) and radius \(R\) is moving with velocity \(v\) through a cloud of particles of density \(\rho\). If all the particles that collide with the star are trapped by it, show that the mass of the star will increase at a rate
\[\frac{dM}{dt} = \pi\rho v(R^2 + \frac{2GMR}{v^2}).\]Solution:
It is easier to use a moving reference frame with velocity v, centered at the star. This allows for mathematical convenience in dealing with the problem. Thus the star is stationary, and dust particles are moving towards it with velocity \(v\).
We want to try to find a thin cylinder whose axis lies along the axis of movement of the star, in which all the particles lying inside it will collide with the star after a time differential \(dt\). So what we start with is basically finding the minimum distance of approach of any particle, since the star’s gravitational field attracts particles in all directions. If this distance of approach is less than \(R\), then we know there will be a collision. From there we can enforce the largest acceptable distance of approach to be \(R\), and hence find the radius of the cylinder slab for which all particles inside will collide with the star.
By the law of conservation of energy and that of angular momentum under central conservative forces, we have the following radial energy equation:
\[E = \frac{1}{2}mv^2 = \frac{1}{2}\dot{r}^2 + \frac{J^2}{2mr^2} - \frac{GMm}{r}\]Plugging in \(\dot{r} = 0\) since we want the closest distance of approach, and rearranging this we get:
\[r^2 - 2ar + b^2 = 0, a = \frac{-GMm}{rmv^2}\]Which yields:
\[r = \frac{-GM}{v^2} + \sqrt{(\frac{GM}{v^2})^2 + b^2}\]Rearranging then squaring both sides yields:
\[b^2 = r^2 + \frac{2GMr}{v^2}\]Where \(b\) is the impact parameter. From here, we realize that the maximum closest distance of approach acceptable to guarantee a collision is \(R\). Hence, the maximum impact parameter that guarantees a collision satisfies the equation:
\[b_{max}^2 = R^2 + \frac{2GMR}{v^2}\]Visualizing the impact parameter, we see that all particles with impact parameters less than \(b_{max}\) will collide with the star, hence all particles in a cylinder of surface area \(\pi b_{max}^2\) and height \(vdt\) will collide with the star in a time differential \(dt\). Multiplying this volume with the density \(\rho\) we get the mass that will be added to the star in a time differential \(dt\).
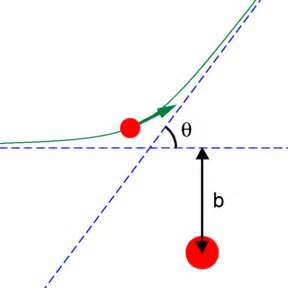Impact parameter visualized - Wikipedia
Combining this yields the required equation:
\[dM = \pi\ \rho(vdt)\ b_{max}^2 = \pi\ \rho(vdt)\ (R^2 + \frac{2GMR}{v^2})\]Finally:
\[\frac{dM}{dt} = \pi\rho v(R^2 + \frac{2GMR}{v^2}).\]
Ch.4 P29 - Scattering Problem
Part 1
An \(\alpha\) particle of energy 4keV (\(1eV = 1.6 * 10^{-19}J\)) is scattered by an aluminum atom through an angle of \(90^{\circ}\). Calculate the distance of closest approach to the nucleus. (Atomic number of \(\alpha\)-particle = 2, atomic number of Al = 13, \(e = 1.6 * 10^{-19}C\).)
Solution: We know that:
\[b = a*cot(\frac{\theta}{2}), a = \frac{q_1*q_2}{4\pi\epsilon_0mv^2}cot(\frac{\theta}{2}) = \frac{(Z_\alpha e)(Z_{Al}e)}{4\pi\epsilon_0mv^2}cot(\frac{\theta}{2}) = \frac{Z_\alpha Z_{Al}e^2}{4\pi\epsilon_0mv^2}cot(\frac{\theta}{2})\]Also, we are given the energy of the \(\alpha\)-particle hence we can find \(mv^2\) and replace to find \(a, b\).
\[E = \frac{1}{2}mv^2 = 4keV \implies mv^2 = 8keV\]What remainds is to find the distance of closest approach. As in the previous exercise, we can find the distance of closest approach using the following formula since the same conservation laws apply:
\[d = a + \sqrt{a^2 + b^2}\]This yields the required answer of \(1.13*10^{-11}m\).
Part 2
A beam of such particles with a flux of \(3*10^8 m^{-2}s^{-1}\) strikes a target containing \(50 mg\) of aluminum. A detector of cross-sectional area \(400mm^2\) is placed \(0.6m\) from the target in a direction at right angles to the beam direction. Find the rate of detection of \(\alpha\)-particles. (Atomic mass of Al \(= 27u; 1u = 1.66*10^{-27}kg.\))
Solution:
Using the derivations in chapter 4, this exercise is solved by simply replacing values.
\[dw = Nf\frac{d\sigma}{d\omega}\frac{dA}{L^2}\]We find the following:
\[\theta = 90^{\circ} d\omega = sin(\theta)d\theta d\phi = d\theta d\phi \\ d\sigma = \frac{a^2 cos(\frac{\theta}{2}) d\theta d\phi}{2sin^3(\frac{\theta}{2})} = a^2d\theta d\phi \\ f = 3*10^8 m^{-2}s^{-1} (given) \\ N = \frac{50*10^{-6} kg}{27*1.66*10^{-27}} = 1.115*10^{21} L = 0.6m (given) A = 400mm^2 = 400*10^{-6}m^2\]After replacement, we finally get:
\[w = \frac{Nfa^2}{L^2} \int dA = \frac{Nfa^2 A}{L^2} = 8.1*10^3s^{-1}\]
Ch.4 Problem 11 - Electromagnetic Field Effect on Charged Particle
Part 1
Write down the equation of motion for a charged particle in uniform parallel electric and magnetic fields, both in the z-direction, and solve it given that the particle starts from the origin with velocity \((v, 0, 0)\).
Solution:
Given that:
\(\dot{\textbf{r}}_0 = (v, 0, 0)\)
\(\textbf{r} = (0, 0, 0)\)
\(\textbf{E} = E\textbf{k} , \textbf{B} = B\textbf{k}\)
We begin by writing down the equation of motion:
\[m\ddot{\textbf{r}} = q\textbf{E} + q\dot{\textbf{r}}\wedge \textbf{B}\]Breaking it down we get the following ODEs:
\[\ddot{x} = \frac{qB}{m}\dot{y}\\ \ddot{y} = \frac{-qB}{m}\dot{x}\\ \ddot{z} = \frac{qB}{m}\]To solve these differential equations, we use an extra variable \(\phi\) such that:
\[\phi = \dot{x}\]Then we get:
\[\dot{\phi} = \frac{qB}{m}\dot{y}\\ \ddot{\phi} = \frac{qB}{m}\ddot{y} = \frac{qB}{m}(\frac{-qB}{m}\phi)\]Which is equivalent to:
\[\ddot{\phi} + (\frac{qB}{m})^2\phi = 0\]The solution to this ODE is simply \(\phi = v*cos(\frac{qB}{m}t)\). (Constants found using initial position and velocity values given.)
Hence:
\[\dot{x} = v*cos(\frac{qB}{m}t)\\ x = \frac{mv}{qB}sin(\frac{qB}{m}t)\]and:
\[\dot{y} = -v*sin(\frac{qB}{m}t)\\ y = \frac{mv}{qB}(cos(\frac{qB}{m}t) - 1)\]as for \(\ddot{z}\) it is simply:
\[\dot{z} = \frac{qE}{m}t\\ \ddot{z} = \frac{qE}{2m}t^2\]Part 2
A screen is placed at \(x=a\), where \(a<<mv/qB\). Show that the locus of points of arrival of particles with given \(m\) and \(q\), but different speeds \(v\), is approximately a parabola. How does this locus depend on \(m\) and \(q\)?
To be continued.